Teorema del confronto

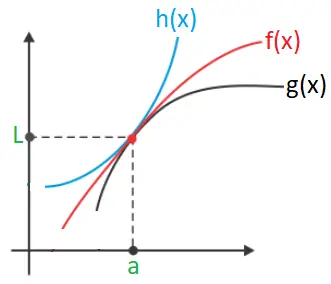
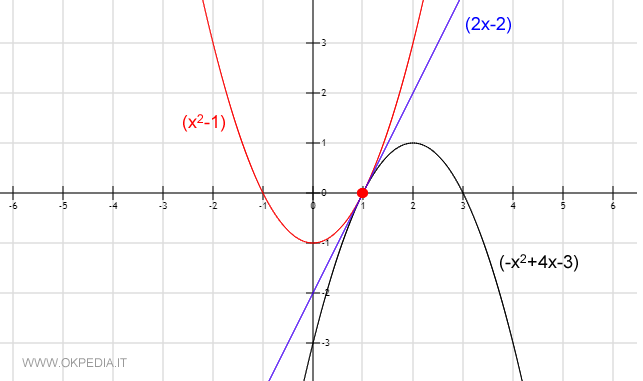
Il teorema del confronto è un teorema di analisi matematica. Assume forme diverse a seconda del contesto, e permette di calcolare il limite di una successione o funzione confrontando questa con altri due oggetti analoghi che "si stringono sempre di più" intorno a quello dato.

È informalmente chiamato teorema dei due carabinieri, per un'allegoria: il teorema sarebbe rappresentato da due carabinieri (due funzioni o successioni ${\displaystyle a,c}$ che si stringono sempre di più) che conducono in arresto un prigioniero (una funzione o successione ${\displaystyle b}$): questo "tende" sicuramente allo stesso punto dove tendono i carabinieri (il limite comune di ${\displaystyle a}$ e ${\displaystyle c}$). Sulla base di considerazioni simili, il teorema è talvolta detto anche teorema del sandwich o teorema di compressione.

Successioni

Il teorema del confronto per le successioni asserisce che se ${\displaystyle \{a_{n}\},\{b_{n}\}}$ e ${\displaystyle \{c_{n}\}}$ sono tre successioni di numeri reali tali che definitivamente (cioè per ${\displaystyle n}$ sufficientemente grande)

${\displaystyle a_{n}\leq b_{n}\leq c_{n}}$

e se si ha

${\displaystyle \lim _{n\to \infty }a_{n}=\lim _{n\to \infty }c_{n}=l,}$

allora anche

${\displaystyle \lim _{n\to \infty }b_{n}=l.}$

Dimostrazione

Dalla definizione di limite di una successione, si ricava che per ogni ${\displaystyle \varepsilon >0}$ esistono ${\displaystyle N,N'}$ tali che:

${\displaystyle l-\varepsilon N,}$

${\displaystyle l-\varepsilon N'.}$

Quindi per ogni ${\displaystyle n}$ maggiore di ${\displaystyle M=\max\{N,N'\}}$ si ottiene:

${\displaystyle l-\varepsilon$

Quindi per ogni ${\displaystyle \varepsilon >0}$ esiste un ${\displaystyle M}$ tale che:

${\displaystyle l-\varepsilon M.}$

In altre parole, la successione ${\displaystyle b_{n}}$ tende a ${\displaystyle l}$.

Esempi

La successione:

${\displaystyle b_{n}={\sin n\cos n \over n^{2}}}$

è "stretta" fra le successioni:

${\displaystyle a_{n}=-{\frac {1}{n^{2}}},\qquad \ c_{n}={\frac {1}{n^{2}}}}$

poiché

${\displaystyle -1\leq \sin n\cos n\leq 1}$

implica

${\displaystyle -{\frac {1}{n^{2}}}\leq {\sin n\cos n \over n^{2}}\leq {\frac {1}{n^{2}}},}$

per ogni ${\displaystyle n}$. Entrambe ${\displaystyle a_{n}}$ e ${\displaystyle c_{n}}$ sono infinitesime (convergono cioè a zero), e quindi per il teorema del confronto anche ${\displaystyle b_{n}}$ è infinitesima.

Corollario

Teoremi di confronto si possono applicare anche per i limiti infiniti. Se ${\displaystyle \{a_{n}\},\{b_{n}\}}$ sono due successioni tali che:

${\displaystyle a_{n}\leq b_{n}}$

per ogni ${\displaystyle n}$, e se

${\displaystyle \lim _{n\to \infty }a_{n}= \infty ,}$

allora anche

${\displaystyle \lim _{n\to \infty }b_{n}= \infty .}$

Oppure se

${\displaystyle a_{n}\leq b_{n},}$

per ogni ${\displaystyle n}$, e se

${\displaystyle \lim _{n\to \infty }b_{n}=-\infty ,}$

allora anche

${\displaystyle \lim _{n\to \infty }a_{n}=-\infty .}$

Dimostrazione Corollario

Per ipotesi ${\displaystyle \lim _{n\to \infty }a_{n}= \infty }$ e pertanto, dalla definizione di limite di una successione, per ogni ${\displaystyle M>0}$ esiste un numero naturale ${\displaystyle N}$ tale che ${\displaystyle a_{n}>M}$ per ogni ${\displaystyle n>N}$.

Dato che ${\displaystyle b_{n}\geq a_{n}}$ per ogni ${\displaystyle n}$ si ottiene che:

${\displaystyle b_{n}\geq a_{n}>M.}$

Quindi:

${\displaystyle \lim _{n\to \infty }b_{n}= \infty .}$

Funzioni

Il teorema del confronto per le funzioni asserisce che, date tre funzioni ${\displaystyle f,g,h\colon X\to \mathbb {R} }$ definite su un dominio ${\displaystyle X}$ di ${\displaystyle \mathbb {R} }$, e dato un punto di accumulazione ${\displaystyle x_{0}}$ per ${\displaystyle X}$, se:

${\displaystyle \lim _{x\to x_{0}}f(x)=\lim _{x\to x_{0}}h(x)=l}$

ed esiste un intorno ${\displaystyle U}$ di ${\displaystyle x_{0}}$ tale che

${\displaystyle f(x)\leq g(x)\leq h(x),\qquad \forall x\in U\cap X\backslash \left\{x_{0}\right\},}$

allora

${\displaystyle \lim _{x\to x_{0}}g(x)=l.}$

Dimostrazione

Per la definizione di limite, per ogni ${\displaystyle \varepsilon >0}$ esistono due intorni ${\displaystyle U_{1}}$ e ${\displaystyle U_{2}}$ di ${\displaystyle x_{0}}$ tali che:

${\displaystyle l-\varepsilon$

${\displaystyle l-\varepsilon$

Quindi

${\displaystyle l-\varepsilon$

Quindi per ogni ${\displaystyle \varepsilon >0}$ esiste un intorno ${\displaystyle U_{1}\cap U_{2}\cap U}$ tale che

${\displaystyle l-\varepsilon$

In altre parole:

${\displaystyle \lim _{x\to x_{0}}g(x)=l.}$

Esempio

Un'applicazione importante di questo teorema è la verifica del limite:

${\displaystyle \lim _{x\to 0}{\frac {\sin x}{x}}=1.}$

Si prenda come riferimento l'immagine a destra. Sia ${\displaystyle 0$ la misura in radianti dell'arco di circonferenza di centro O e raggio unitario.

Allora

${\displaystyle {\overline {PH}}=\sin x,\qquad {\overline {QA}}=\tan x}$

Ne segue che

${\displaystyle \sin x$

da cui, dividendo per ${\displaystyle \sin x}$

${\displaystyle 1<{\frac {x}{\sin x}}<{\frac {1}{\cos x}}}$

prendendo i reciproci

${\displaystyle \cos x<{\frac {\sin x}{x}}<1}$

sapendo che la disuguaglianza non cambia per ${\displaystyle -x}$ e che

${\displaystyle \lim _{x\to 0}\cos x=1,}$

sfruttando il teorema del confronto si ottiene:

${\displaystyle \lim _{x\to 0}{\frac {\sin x}{x}}=1.}$

Bibliografia

• G. C. Barozzi, Primo corso di analisi matematica, Bologna, Zanichelli, 1998. ISBN 88-080-1169-0.
• (EN) Stewart, James (2008). Multivariable Calculus (6th ed.). pp. 909–910. ISBN 0495011630.

Voci correlate

• Funzione (matematica)
• Limite di una successione
• Limite di una funzione
• Punto di accumulazione
• Successione (matematica)

Altri progetti

• Wikimedia Commons contiene immagini o altri file sul teorema del confronto

Collegamenti esterni

• carabinieri, teorema dei, in Enciclopedia della Matematica, Istituto dell'Enciclopedia Italiana, 2013.
• (EN) Eric W. Weisstein, Squeezing Theorem, su MathWorld, Wolfram Research.
• (EN) Squeeze Theorem by Bruce Atwood (Beloit College) after work by, Selwyn Hollis (Armstrong Atlantic State University), the Wolfram Demonstrations Project.